Solve X 3 3xy 2 Dx Y 3 3x 2y Dy Sarthaks Econnect Largest Online Education Community
0 votes 1 answer Show that the set of curves intersect orthogonally x^3 – 3xy^2 = – 2 and 3x^2y – y^3 = 2 asked in Derivatives by RahulYadav (531k points)Given, (x−y 3)dx3xy 2dy=0 Divide above equation by xdx 3y 2dxdy − xy 3 =−1 −(1) let y 3=t
X(x^3-y^3)+3xy(x-y) solution
X(x^3-y^3)+3xy(x-y) solution- Tính giá trị của biểu thức P=x^3y^33xy biết xy=1 Cho xy=1 Tính giá trị của a) P = x3 y3 3xy P = x 3 y 3 3 x y b) Q = x3 y3 3xy(x2 y2) 6x2y2 (x y) Q = x 3 y 3 3 x y ( x 2 y 2) 6 x 2 y 2 ( x y) Theo dõi Vi phạm Toán 8 Bài 3 Trắc nghiệm Toán 8 Bài 3 Giải bài tập Toán 8 Bài 3 Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence pro
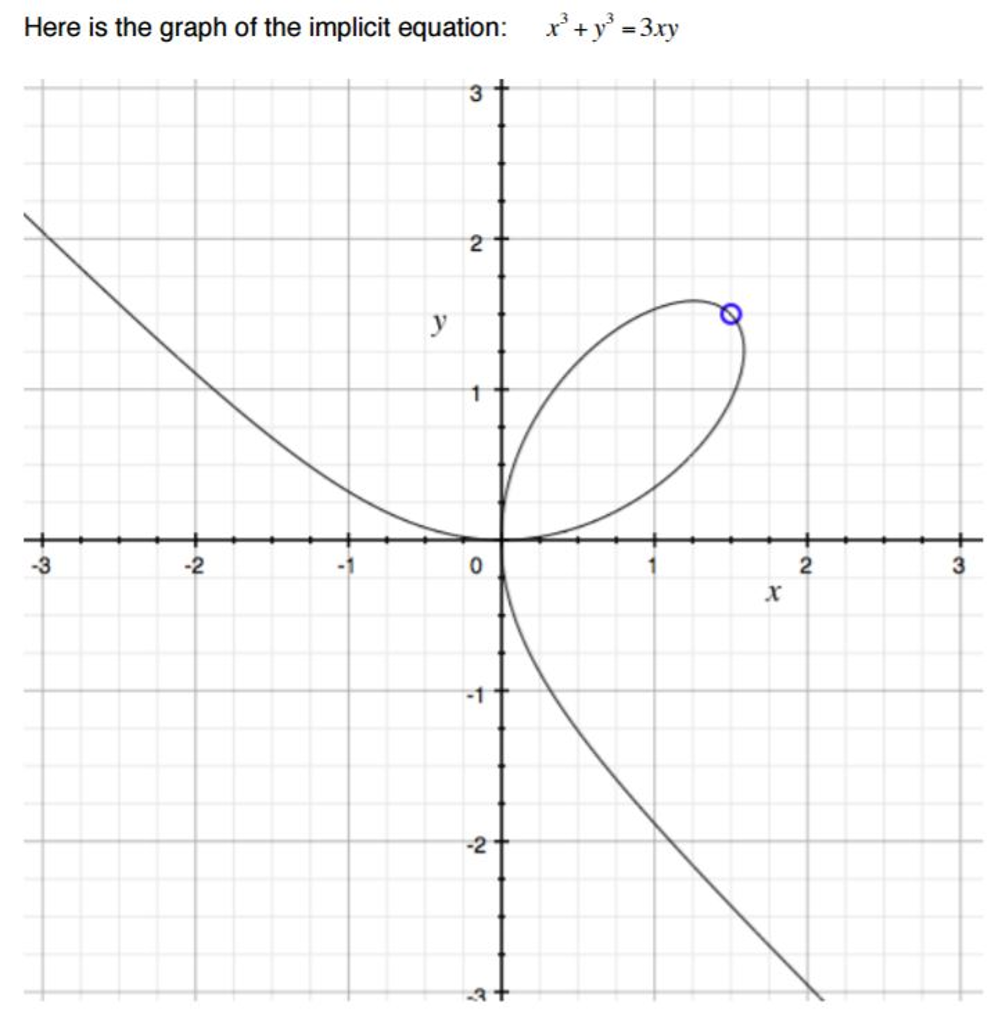
Solved Here Is The Graph Of The Implicit Equation X 3 Y 3 Chegg Com
Answer k=3 Stepbystep explanation we know that A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form or In this problem we have therefore The constant of proportionality is k=3 quarterfreelp and 26 more users found this answer helpfulFall 13 S Jamshidi 4 x4 y4 z4 =1 If x,y,z are nonzero, then we can consider Therefore, we have the following equations 1 1=2x2 2 1=2y2 3 1=2z2 4 x4 y4 z4 =1 Remember, we can only make this simplification if all the variables are nonzero!X y is a binomial in which x and y are two terms In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2
#(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#(xyz)^3 (x y z)(x y z)(x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy y * y = y^2 y * z = yz z * x = xz z * y = yz z * z = z^2 x^3 y^3 z^3 3x^2y 3xy^2 3x^2z 3z^2x 3y^2z 3z^2y 6xyz Lennox Obuong Algebra StudentConsider the function f(x;y) = 3 p x2y Show that the directional derivative exists at the origin (by letting ~u= hcos( );sin( )iand using the de nition), BUT, fis not di erentiable at the origin (because if it were, we could use rf~uto compute D ~uf) SOLUTION Compute the directional derivative at the origin by using the de nition D uf(0;0
X(x^3-y^3)+3xy(x-y) solutionのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
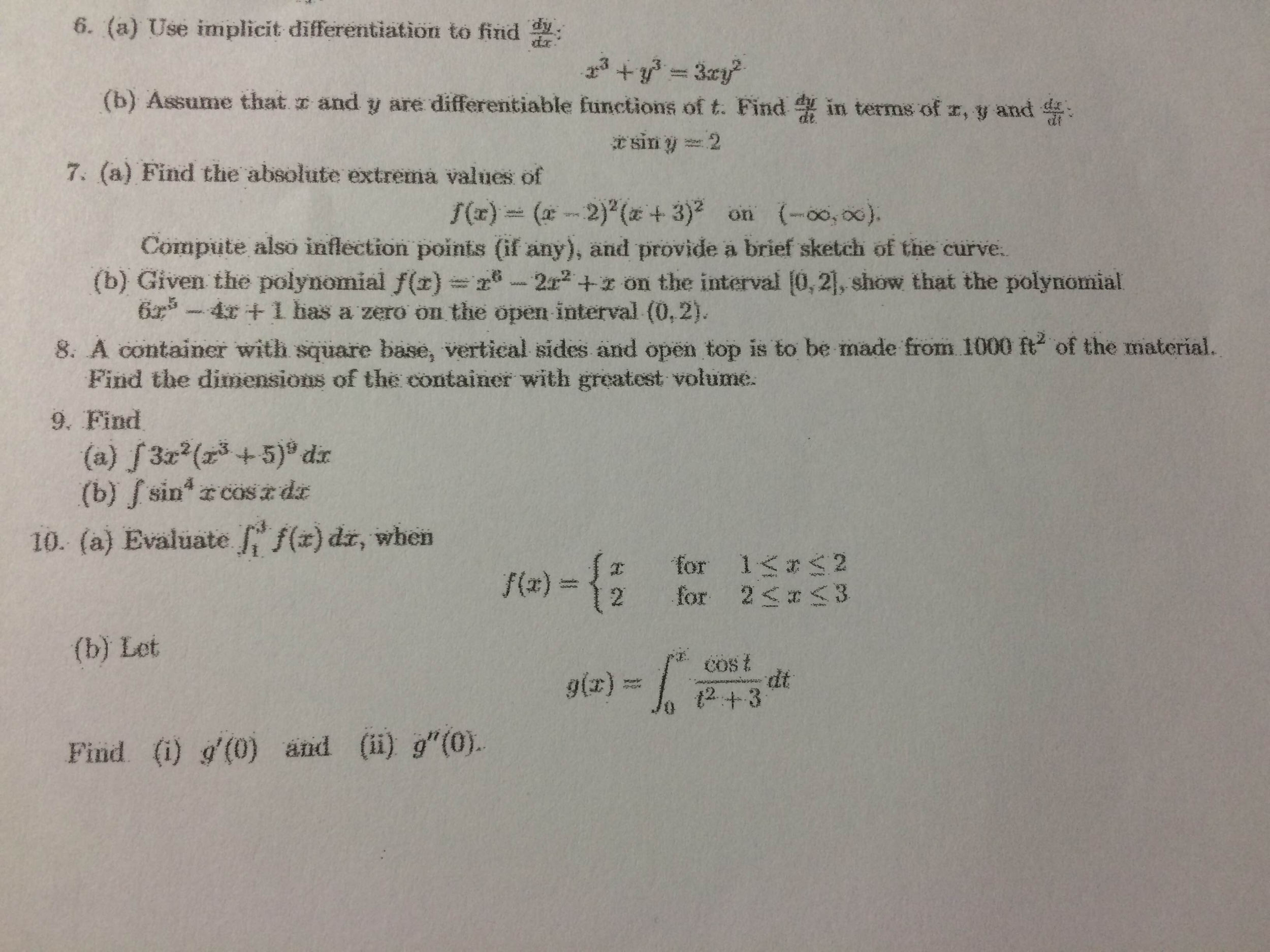 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | 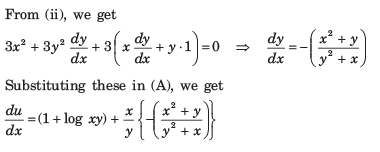 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download | 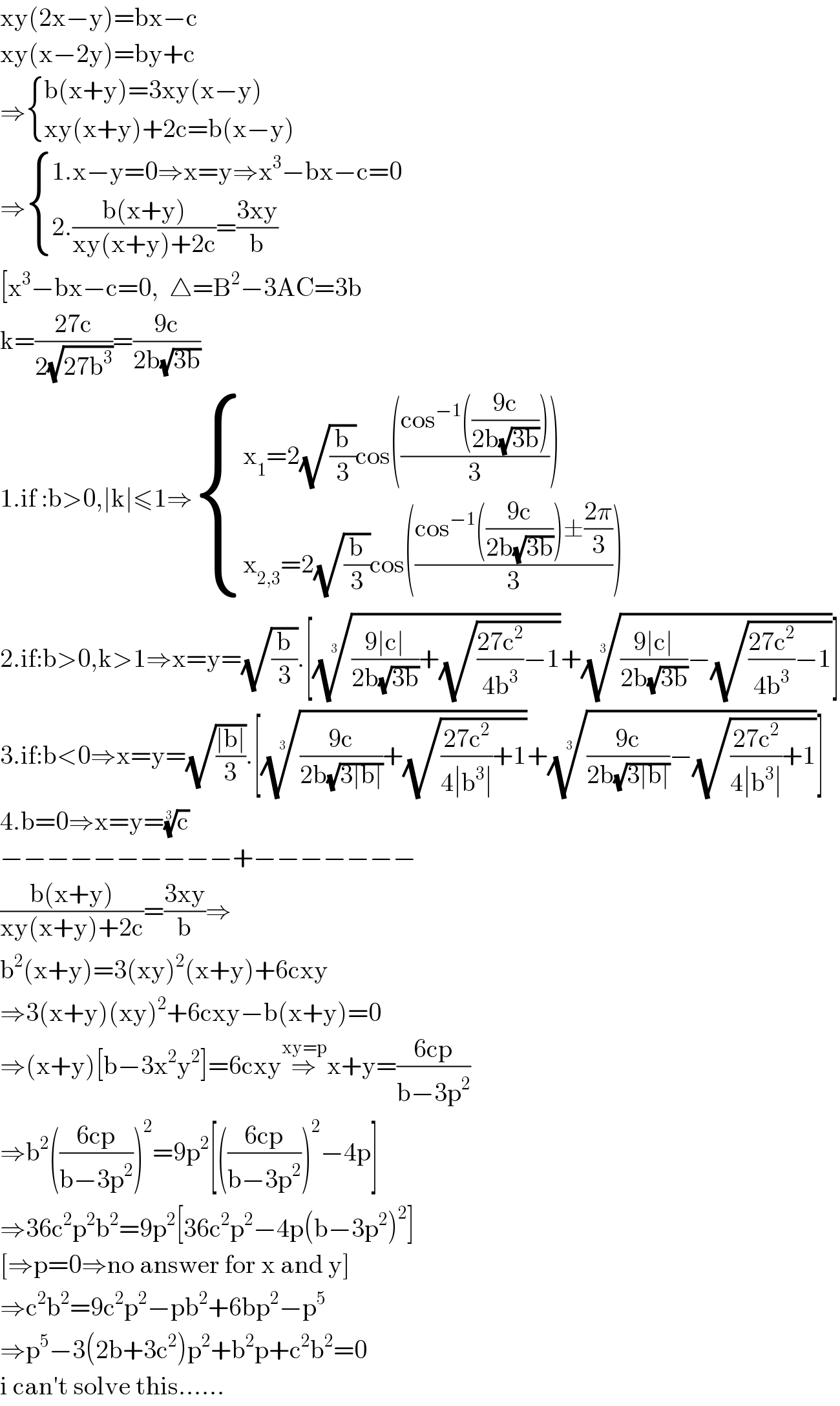 Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | 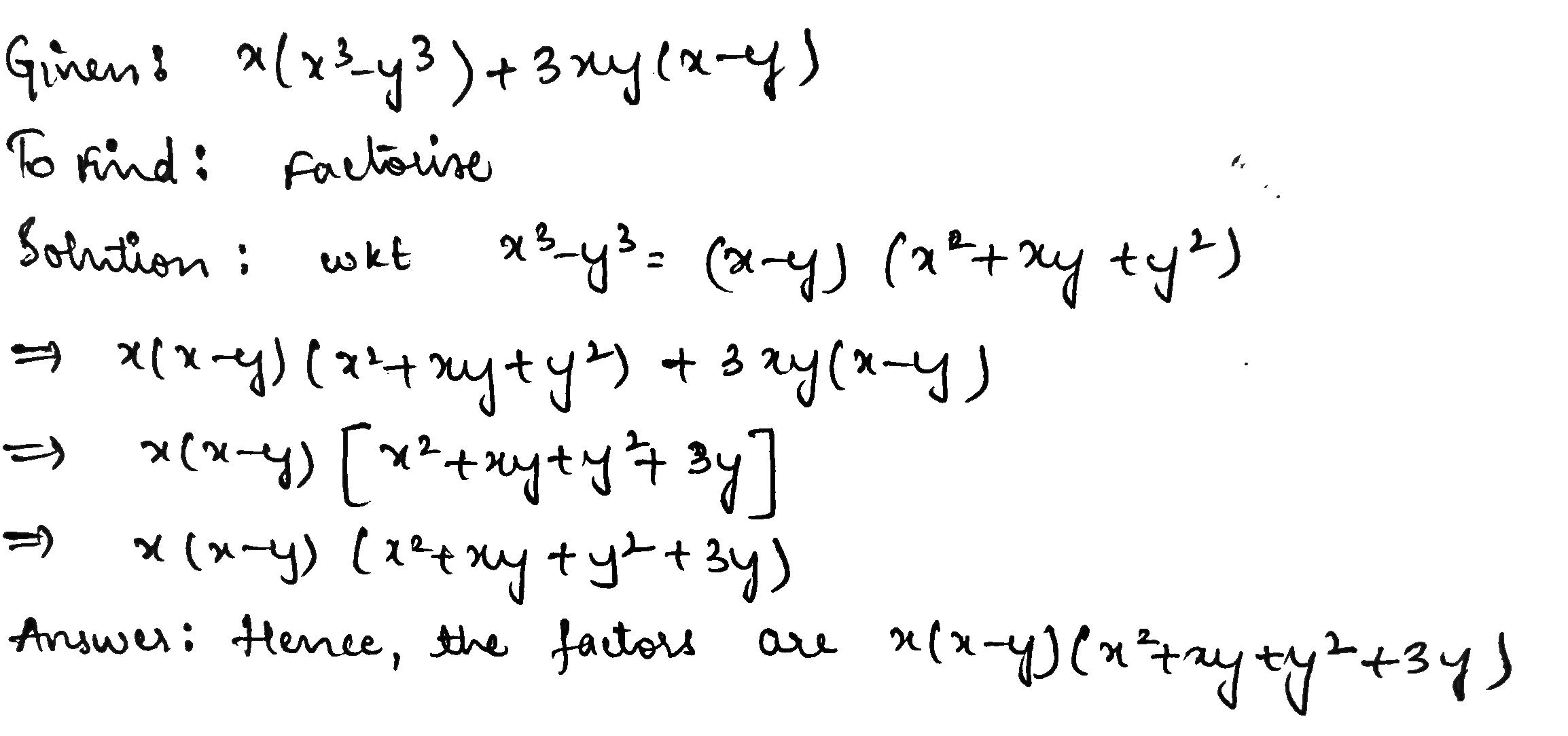 Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |
.png) Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | 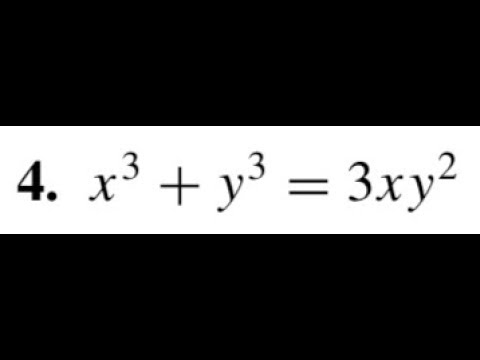 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download | 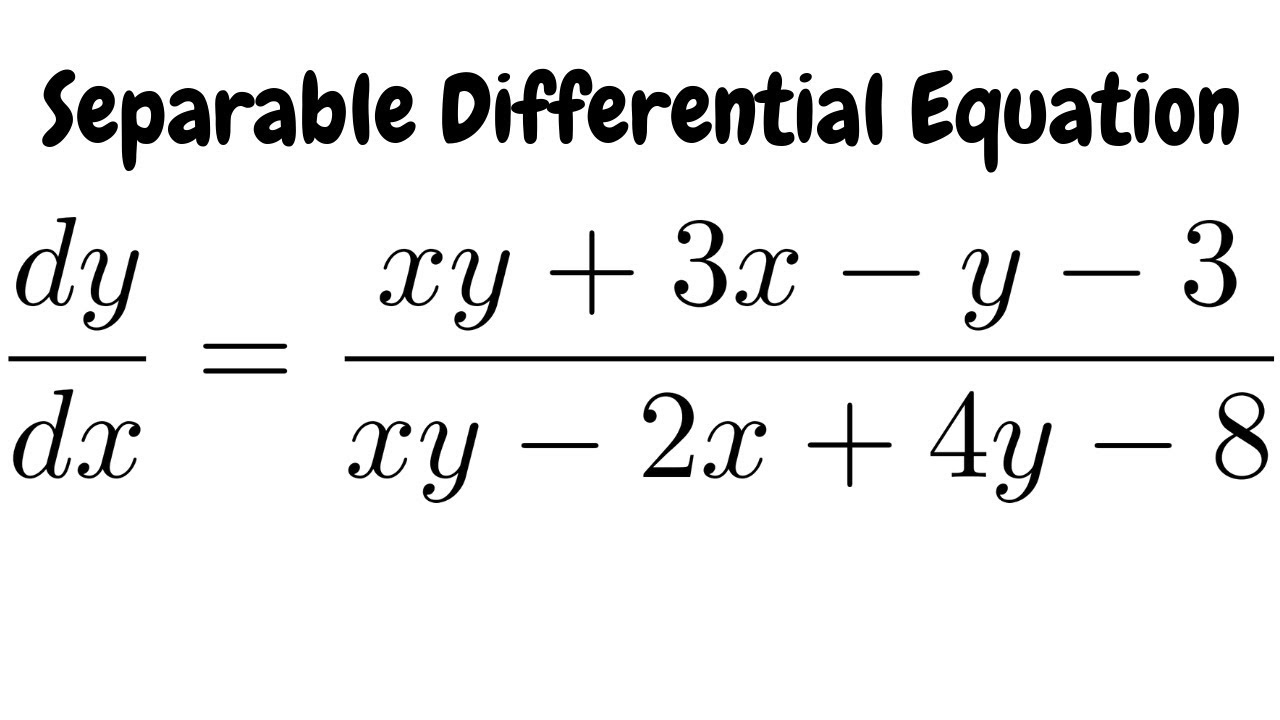 Systems Engineering And Analysis Ppt Download |
Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download | 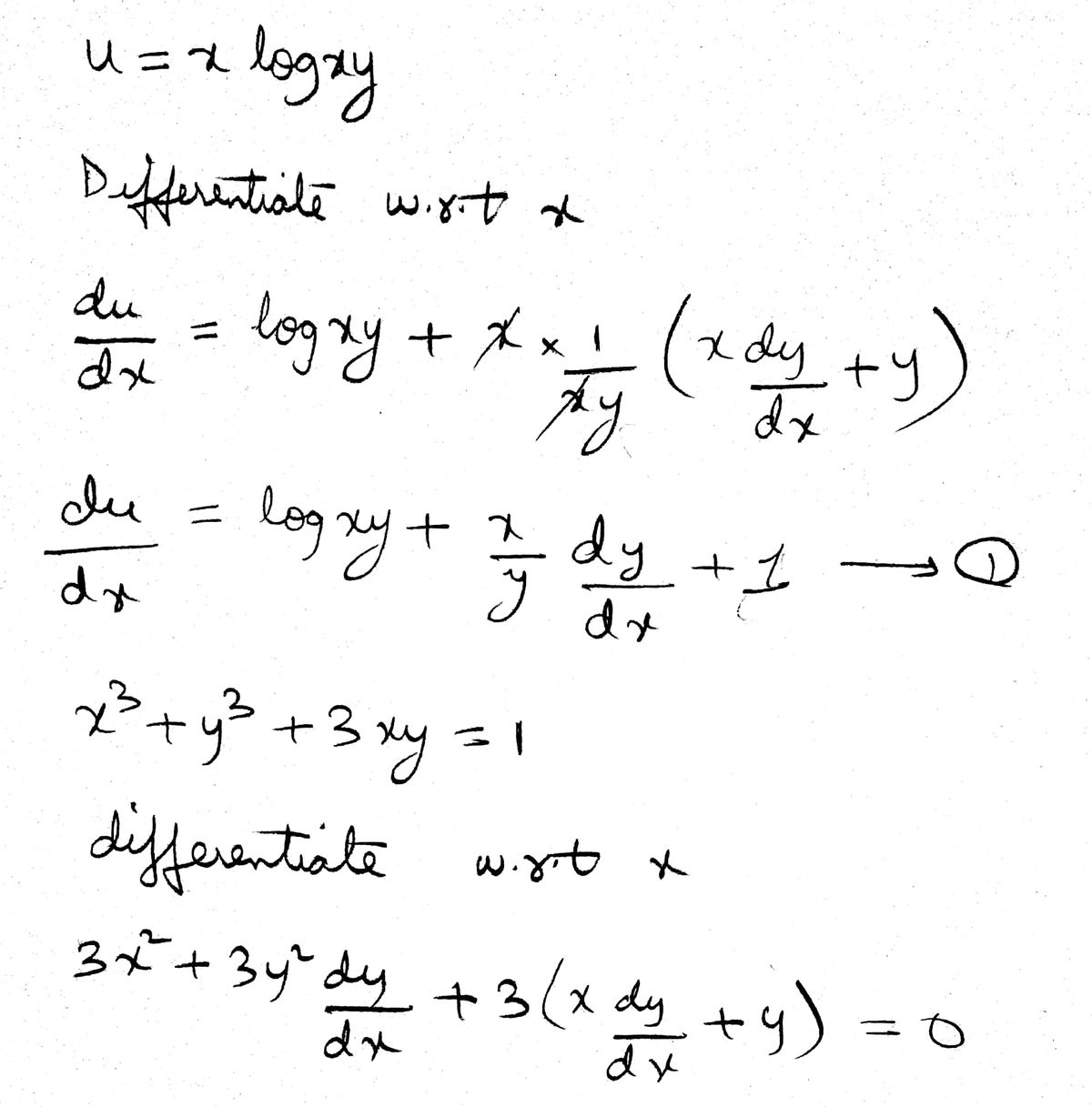 Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | 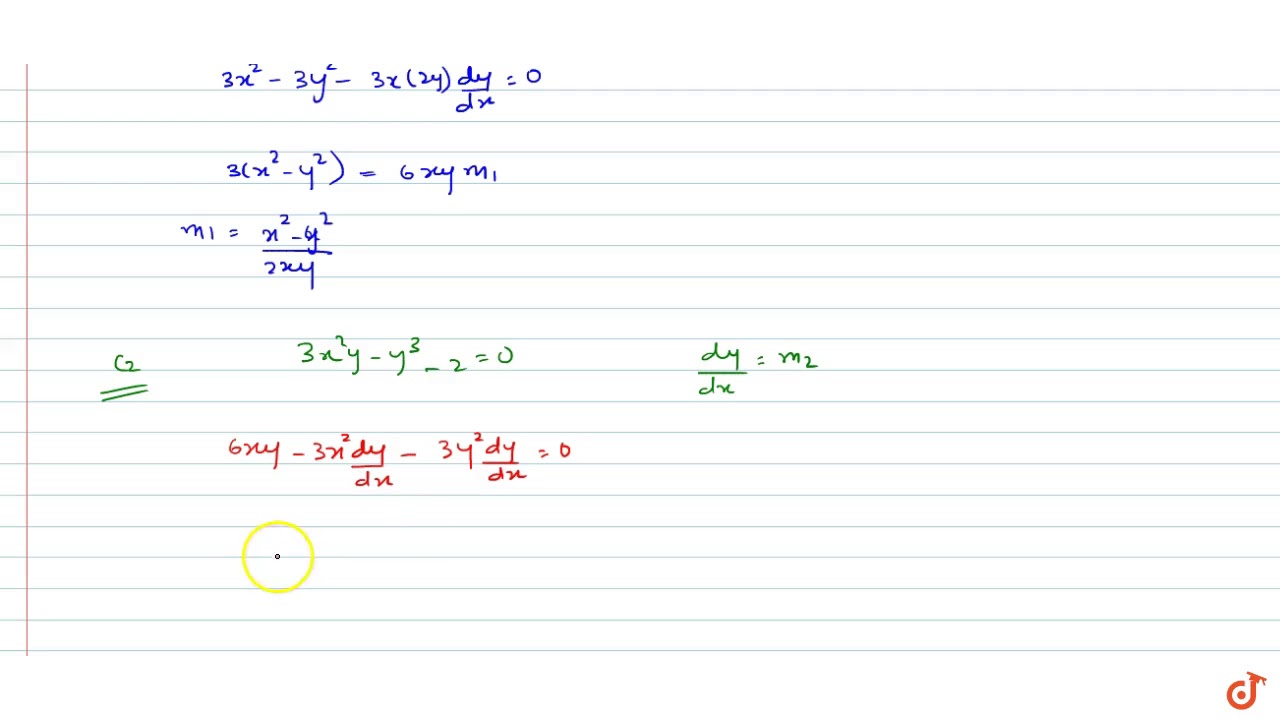 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
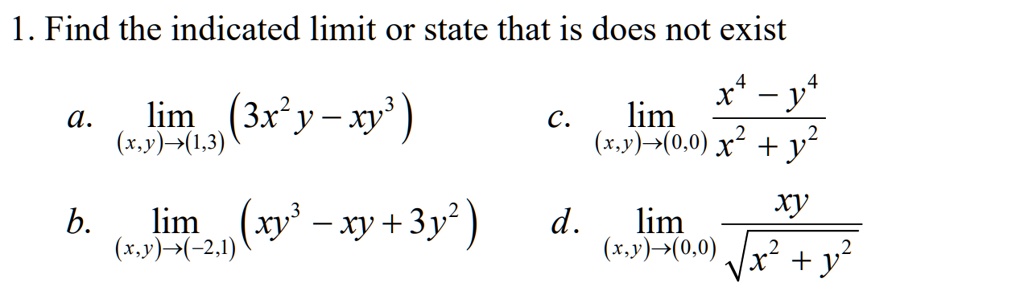 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | 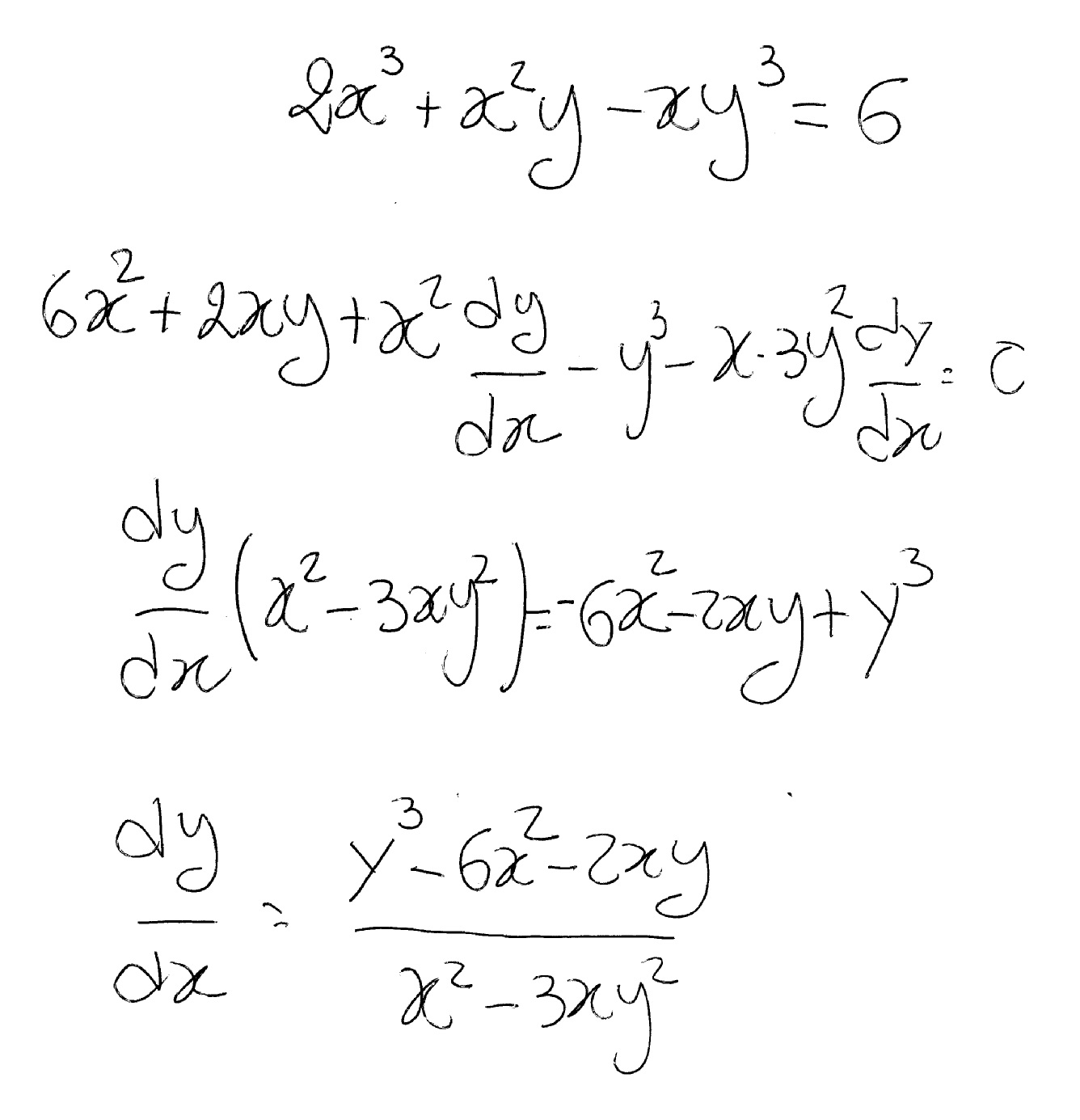 Systems Engineering And Analysis Ppt Download | 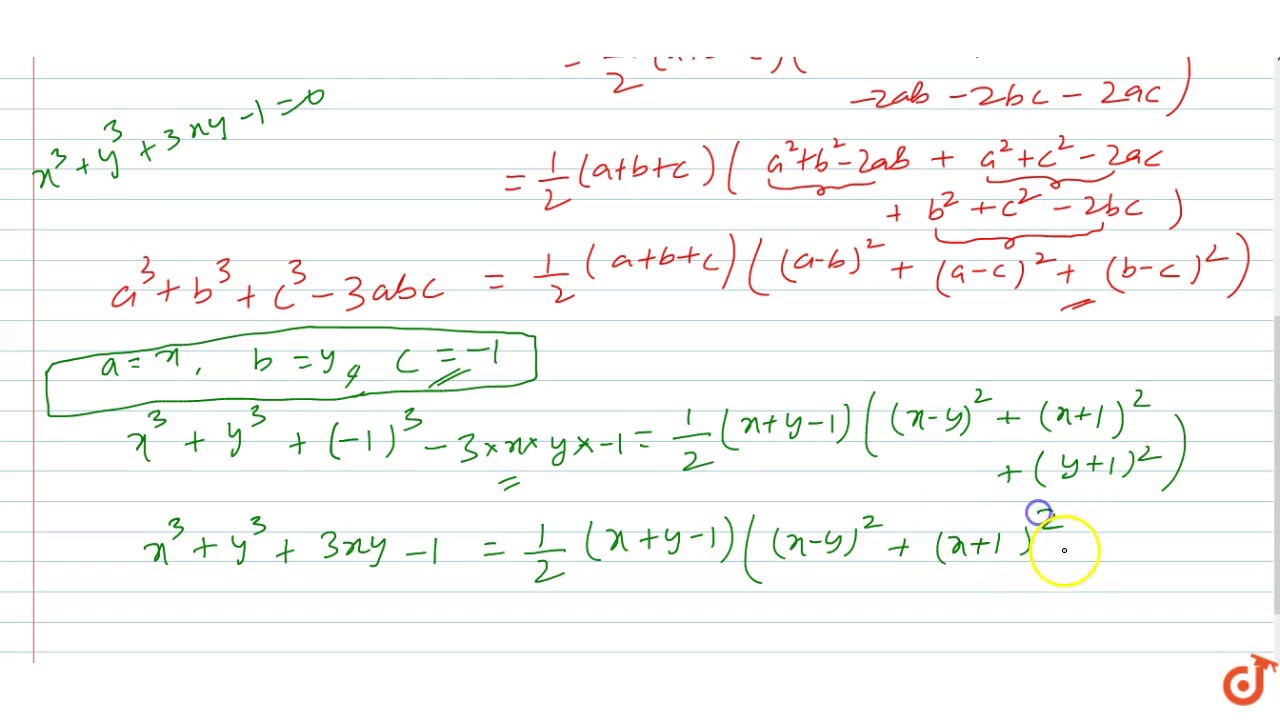 Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download | Systems Engineering And Analysis Ppt Download | 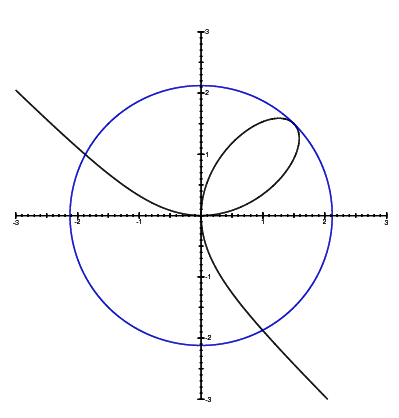 Systems Engineering And Analysis Ppt Download |
 Systems Engineering And Analysis Ppt Download |  Systems Engineering And Analysis Ppt Download |
Ejercicios EDO's de primer orden 3 1 y3 dy = dx x2 Z y−3 dy = Z x−2 dx, 1 −2 y−2 = −x−1 c 1, −1 2y2 −1 x c 1, 1 y2 2 x c, c = −2c 1 Solución implícita 1 y2 2xc x Solución explícita y = ±View Homework Help hw12soln from MATH 2940 at Cornell University 181 19) Let x3 y 3 = 3xy be the folium of Descartes (a) Show that the folium has a
Incoming Term: (x+y)^3=x^3+y^3+3xy(x+y), x(x^3-y^3)+3xy(x-y) solution, (x+y)3=x3+y3+3xy(x+y),




0 件のコメント:
コメントを投稿